

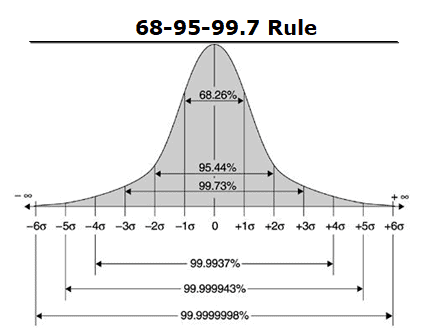
The challenging part, indeed, is figuring out whether the distribution is normal or not. Since all we need to describe any normal distribution is the mean and standard deviation, this rule holds for every normal distribution in the world! Knowing this rule makes it very easy to calibrate your senses. So, the chance of seeing someone with a height between 65 and 68.5 inches would be: _.ģ4%! It's exactly the same as our first example. Try doing the same for female heights: the mean is 65 inches, and standard deviation is 3.5 inches. Remember, you can apply this on any normal distribution. So the outer edges (that is, heights below 58 and heights above 82) together make (100% - 99.7%) = 0.3%. Here, we use also the final property: everything must sum to 100%. Both outer edges have the same %.Īnd now your final (and hardest test): What's the chance of seeing someone with a height greater than 82 inches? What's the chance of seeing someone with a height between 62 and 66 inches? It's 34%! We leverage both the properties: the distribution is symmetric, which means chances for (66-70) inches and (70-74) inches are both 68/2 = 34%. What's the chance of seeing someone with a height between between 5 feet 10 inches and 6 feet 2 inches? (That is, between 70 and 74 inches.) Now for the fun part: Let's apply what we've just learned. To continue our example, the average American male height is 5 feet 10 inches, with a standard deviation of 4 inches. It says: 68% of the population is within 1 standard deviation of the mean.ĩ5% of the population is within 2 standard deviation of the mean.ĩ9.7% of the population is within 3 standard deviation of the mean. The 68-95-99 rule is based on the mean and standard deviation. The graph of a Gaussian is a characteristic symmetric 'bell curve' shape. It is named after the mathematician Carl Friedrich Gauss. Together, the mean and the standard deviation make up everything you need to know about a distribution. In mathematics, a Gaussian function, often simply referred to as a Gaussian, is a function of the base form and with parametric extension for arbitrary real constants a, b and non-zero c.

And even fewer are three standard deviations away (or further). Fewer observations are two standard deviations from the mean. Most observations fall within one standard deviation of the mean. This tells you how rare an observation would be. For example, the average of these three numbers: 1, 2, 3 = (1 + 2 + 3) / 3 = 2 Most people just call this "the average." It's what you get if you add up the value of all your observations, then divide that number by the number of observations. There's equal mass before and after the peak.Īnother important property is that we don't need a lot of information to describe a normal distribution. You can reduce lots of complicated mathematics down to a few rules of thumb, because you don't need to worry about weird edge cases.įor example, the peak always divides the distribution in half. This distribution is exciting because it's symmetric – which makes it easy to work with. A lot of things follow this distribution, like your height, weight, and IQ. They are represented by a bell curve: they have a peak in the middle that tapers towards each edge. Today, we're interested in normal distributions. In some cases, 10x above average is common. Your answers to the two questions above are different, because the distribution of data is different. How often would you expect to meet someone who earns 10x as much as Mason?Īnd now, how often would you expect to meet someone who is 10x as tall as Mason? He's an average American 40-year-old: 5 foot 10 inches tall and earning $47,000 per year before tax. We will write two functions, pdf_gaussian and pf_gaussian where former is a probability density function (pdf) and later is just a gaussian probability function.Meet Mason. Let's now write a function which returns a gaussian distribution given the mean and the standard deviation. $f(x) = \frac$ is known as the normalizing constant and is mainly used to reduce the probability function to a probability density function with total probability of one. The probability density function of a normal distribution is given as However, in this notebook, we will implement the formula by ourselves.
There are many python libraries one can use to generate a normal distribution. Few examples include height of people, newborns’ birth weight, the sum of two dice, etc. Normal distribution is quite ubiquitous in life. The purpose of this notebook is to introduce the Gaussian distribution (also known as normal distribution)- the distribution from which my sample came from. There are some very interesting statistical tests which one could employ to figure this out. In the project I didn't know the actual distribution but had only a sample, and I needed to know from which distribution does the sample comes from. Following notebook is inspired from one of the projects I was pursuing during the final year of my PhD.


 0 kommentar(er)
0 kommentar(er)
